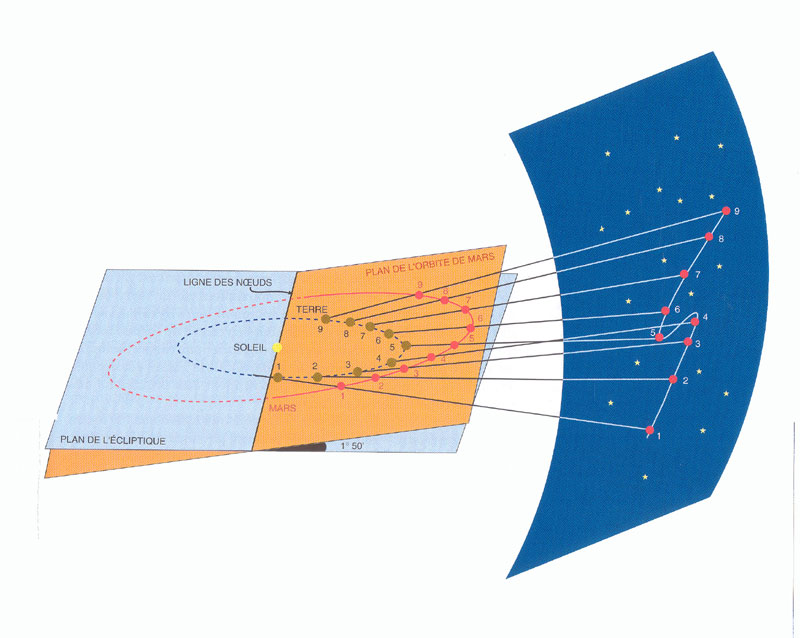
Mouvement apparent de Mars (source : Numéro spécial Pour la Science, Kepler)
Les Lois de Kepler
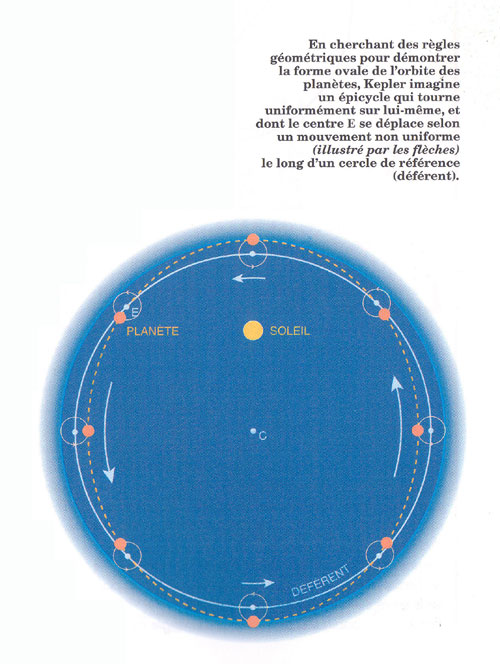
Les deux premières lois paraissent en 1609 dans La nouvelle Astronomie (Astronomia novae). La première élimine l'idée admise depuis les Grecs que le mouvement des planètes était constitué par des cercles ou des sphères (objets « parfaits » par définition), la deuxième se débarrasse de l'idée de mouvement à vitesse constante couramment admise depuis Aristote, enfin la troisième apparaît dans L'harmonie du Monde (Harmonia Mundi) en 1619 et permet de quantifier ces mouvements de manière précise.
Première loi : chaque planète se meut sur une ellipse dont un des foyers est le Soleil.
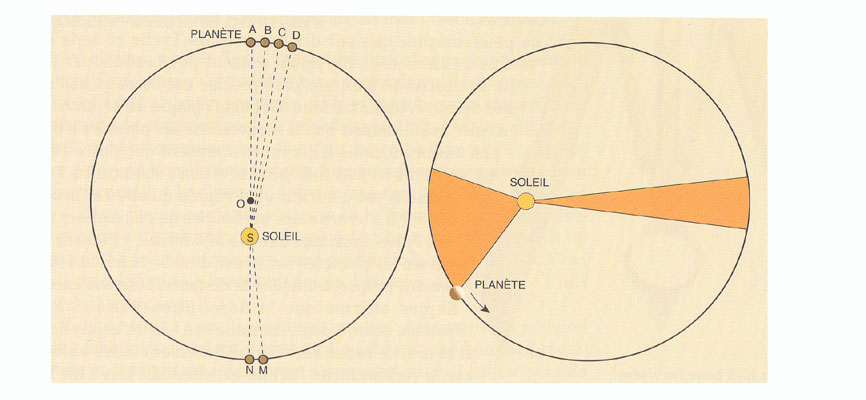
Deuxième loi : les rayons vecteurs des planètes balaient des aires égales en des temps égaux.
Troisième loi : si T est la période de
révolution d'une planète et D sa distance au Soleil, alors 
où k est une
constante.
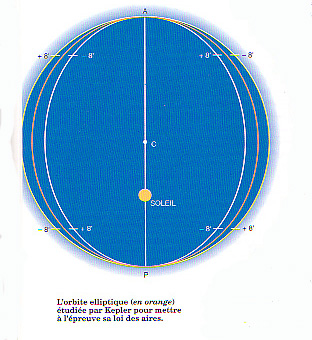
(source : Numéro spécial Pour la Science, Kepler)
Les Lois de Newton
Newton définit donc ses trois lois du mouvement dans son ouvre majeure : Principes mathématiques de la philosophie naturelle (Principia.) publiée en 1687.
Première loi : si un corps est au repos et qu'il n'est soumis à aucune force, alors il restera au repos ; s'il est en mouvement sa trajectoire sera une droite parcourue à vitesse constante.
Deuxième loi : si une force s'exerce sur un corps
de masse m, alors elle fera subir une accélération 
à ce corps de sorte
que 
.
Troisième loi : si un corps A exerce une
force 
sur un corps B,
alors B exerce une force sur A qui est égale en grandeur mais
opposée en direction à 
.
A ces trois lois, valables pour n'importe quels corps,
Newton rajoute la loi de l'attraction universelle : 
, représentant la force exercée entre deux corps de masses m
et m', situés à une distance r l'un de l'autre ; G
étant une constante.
Les illustrations proviennent de http://www-gap.dcs.st-and.ac.uk/~history/BiogIndex.html
Gottfried Wilhem Leibniz
Quelques pages de livres de mathématiques anciens (collection personnelle)
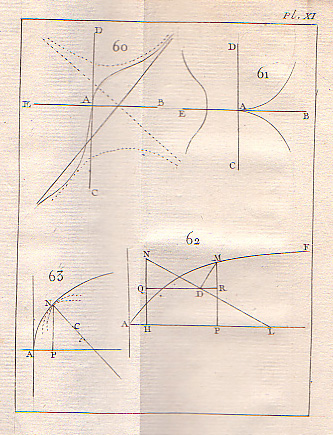
Traité des courbes (1750)
Géométrie de A. M. Legendre (1850)